引子
周末校赛还是一如既往的被锤烂了,其中有一道大家都会的构造题,听说打表找规律很快,但是懒惰的我怎么可能打表呢,于是准备深入研究一下这道题涉及到的数学定理————Dilworth定理。
参考资料
“蔚来杯“2022牛客暑期多校赛 第二场 G-Link with Monotonic Subsequence)
定义
Dilworth定理,一言以蔽之,偏序集能划分成的最少的全序集个数等于最大反链的元素个数(出处:Dilworth定理是个啥东东_狄尔沃斯定理-CSDN博客)。死去的离散数学又开始攻击我了233333。
接下来一个一个来讲解与举例其中的概念。
偏序集
偏序集是由集合 $S$ 与 $S$ 上的偏序关系 $R$ 构成的,记为 $(S,R)$,并非所有元素都必须彼此可比。
偏序关系
对于二元关系 $R⊆S×S$,如果 R 是自反的,反对称的,传递的,那么 R 称为偏序关系,记作≼。它和小于等于的关系是偏序关系是小于等于它爹!小于等于是一个偏序关系。如果两个元素不满足偏序关系可以记作两个元素不可比。
全序集
全序集是一种特殊的偏序集,其中所有元素必须两两可比。
假设有一序列$P = \{p_1, p_2,\dots, p_n\}$, 记集合$S = \{(i, p_i) \mid i \in \mathbb{N}, 1 \leq i \leq n\}$, 偏序关系是$R = \{((i, p_i), (j, p_j)) | i < j且p_i < p_j\}$,$(S, R)$构成一个偏序集。
如果$P$满足$p_i = i$,那么$(S, R)$是一个全序集。但如果$P$形如$P = \{1, 3, 2, 4\}$,其中$(1, 3)$和$(2, 4)$满足偏序关系$R$,但是$(3, 2)$并不满足,此时$(S, R)$就是一个偏序集了。
哈斯图( Hasse 图)
在讲反链之前需要讲一下哈斯图的概念,可以更方便理解其他博客中有的我们也得有!。
哈斯图
维基百科中非常形象的描述,哈斯图是用来表示有限偏序集的一种数学图表,它是一种图形形式的对偏序集的传递简约。
具体的说,对于偏序集合(S, ≼),把S的每个元素表示为平面上的顶点),然后若元素y覆盖x(就是说,x < y并且没有z使得 x < z < y),则绘制从x到y向上的线段或弧线。
懒得自己画图与举例啦,直接开偷,感谢Tofu大佬的例子%%%。
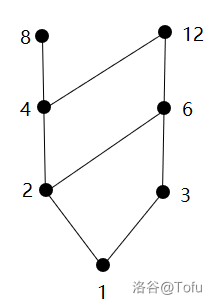
例如,集合 $\{1,2,3,4,6,8,12\}$ 上的关系$ \{ (a,b) | a 整除 b \}$ 画出的哈斯图就是
链与反链
链是偏序集中满足全序集的子集。
反链是偏序集的子集,其中的任意两个元素都不满足偏序关系。
我偷,我再偷
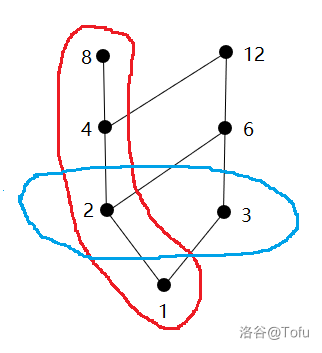
以上面的哈斯图为例,红圈就是一条链,蓝圈就是一条反链。
在这个图中,反链元素个数最多是 2 ,而且,整个图至少需要 2 条链$ ( \{1,2,4,8\} 和 \{3,6,12\}) $来覆盖。
校赛题目
注:此题源自“蔚来杯“2022牛客暑期多校赛 第二场 G-Link with Monotonic Subsequence
First, let’s review some definitions. Feel free to skip this part if you are familiar with them.
A sequence $a$ is a increasing (decreasing) subsequence of a sequence $b$ if $a$ can be obtained from $b$ by deletion of several (possibly, zero or all) elements and all elements are in increasing (decreasing) order from the beginning to the end.
A permutation is an array consisting of $n$ distinct integers from $1$ to $n$ in arbitrary order. For example, $[2,3,1,5,4]$ is a permutation, but $[1,2,2]$ is not a permutation ($2$ appears twice in the array) and $[1,3,4]$ is also not a permutation ($n=3$ but there is $4$ in the array).
The problem starts from here.
Mr.SS has an array. He is currently learning the longest increasing subsequence algorithm. So he comes up with the following question.
Let the value of a permutation $p$ be $max(lis(p),lds(p))$, where $lis(p)$ is the length of the longest increasing subsequence of $p$ and $lds(p)$is the length of the longest decreasing subsequence of $p$. For all permutations of length $n$, which one has the minimum value?
输入描述
Each test contains multiple test cases. The first line contains the number of test cases $T(1 \leq T \leq 1000)$.
For each test case, there is only one line, containing an integer $(1 \leq n \leq 10^6)$.
It is guaranteed that the sum of nnn over all test cases does not exceed $10^6$.
输出描述
For each test case, output a single line containing a permutation of length $n$.
If there are multiple answers, print any of them.
解题思路
- 对于排列$P$记集合$S = \{(i, p_i) \mid i \in \mathbb{N}, 1 \leq i \leq n\}$,偏序关系$R = \{((i, p_i), (j, p_j)) | i < j且p_i < p_j\}$, 那么$(S, R)$即为一个偏序集。
- 考虑如何利用Dilworth定理。全序集就是上升子序列,反链就是下降子序列,因为下降子序列任意两个元素都不满足偏序关系$R$(妙不妙!),下降子序列的最长长度$lds(p)$等于能划分的最少的上升子序列的数目,此时上升子序列中最长长度的最小值即为$lis(p) = \frac {n} {lds(p)}$,$\min\{\max(lis(p), lds(p))\} \equiv lis(p) = lds(p) = \sqrt{n}$。
- 综上所述,我们可以将排列$p$划分为$\sqrt{n}$段,每段的长度为$\sqrt{n}$,倒序输出即可。
AC代码
// Monotonic Subsequence
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
ll T = 1; cin >> T;
while(T -- ) {
ll n; cin >> n;
ll o = ceil(sqrt(n));
ll m = ceil(1.0 * n / o);
ll p = n;
for(ll i = 1; i <= o; i ++ ) {
if(p > m) {
for(ll j = i * m; j > (i - 1) * m; j -- ) {
cout << j << " ";
}
p -= m;
} else {
for(ll j = n; p > 0; j --, p -- ) {
cout << j << " \n"[p == 1];
}
}
}
}
return 0;
}例题 洛谷P1020 [NOIP1999 提高组] 导弹拦截
题面
洛谷这个一键复制markdown我是真喜欢啊[NOIP1999 提高组] 导弹拦截
题目描述
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度,计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
格式
一行,若干个整数,中间由空格隔开。
输出格式
两行,每行一个整数,第一个数字表示这套系统最多能拦截多少导弹,第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
样例 #1
样例输入 #1
389 207 155 300 299 170 158 65样例输出 #1
6 2提示
对于前 $50\%$ 数据(NOIP 原题数据),满足导弹的个数不超过 $10^4$ 个。该部分数据总分共 $100$ 分。可使用$\mathcal O(n^2)$ 做法通过。
对于后 $50\%$ 的数据,满足导弹的个数不超过 $10^5$ 个。该部分数据总分也为 $100$ 分。请使用 $\mathcal O(n\log n)$ 做法通过。对于全部数据,满足导弹的高度为正整数,且不超过 $5\times 10^4$。
此外本题开启 spj,每点两问,按问给分。
NOIP1999 提高组 第一题
$\text{upd 2022.8.24}$:新增加一组 Hack 数据。
解题思路
- 第一问是一个经典问题最长上升(下降)子序列,因为$n$的范围为$1 \leq n \leq 10^5$,所以正常的$dp$的时间复杂度为$\mathcal O(n^2)$是过不了的,可以利用二分优化,具体不展开了。(问:为什么下面的ac代码还有dp的做法呢?答:写着玩2333)
- 第二问就需要用到Dilworth定理了。因为要我们求能划分成的最少的全序集(下降子序列)个数所以直接求最长反链的长度即最长上升子序列即可。离散小波变换°大佬用贪心的思路求第二问,从代码的角度证明了Dilworth定理,详情可以看这里,%%%%。
AC代码
// P1020 [NOIP1999 提高组] 导弹拦截
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
vector<ll> a;
ll n;
ll dp() { // 呜呜dp,我最骄傲的信仰~
vector<ll> dp(n + 1);
for(ll i = 1; i <= n; i ++ ) {
dp[i] = 1;
for(ll j = 1; j < i; j ++ ) {
if(a[j] >= a[i]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
ll ans = -1;
for(ll i = 1; i <= n; i ++ ) ans = max(ans, dp[i]);
return ans;
}
ll yxc() { // yxc教的,有问题问他去
vector<ll> q(n + 1);
q[0] = -1;
ll len = 0;
for(ll i = 1; i <= n; i ++ ) {
ll l = 0, r = len;
while(l < r) {
ll mid = l + r + 1 >> 1;
if(q[mid] >= a[i]) l = mid;
else r = mid - 1;
}
len = max(len, r + 1);
q[r + 1] = a[i];
}
return len;
}
ll solve1() {
vector<ll> b;
for(ll i = 1; i <= n; i ++ ) {
if(b.empty() || b.back() >= a[i]) b.push_back(a[i]);
else *upper_bound(b.begin(), b.end(), a[i], greater<ll>()) = a[i];
}
return b.size();
}
ll solve2() {
vector<ll> b;
for(ll i = 1; i <= n; i ++ ) {
if(b.empty() || b.back() < a[i]) b.push_back(a[i]);
else *lower_bound(b.begin(), b.end(), a[i]) = a[i];
}
return b.size();
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
a.push_back(0);
ll x; while(cin >> x) a.push_back(x);
n = a.size() - 1;
// ll ans = dp();
// ll ans = yxc();
ll ans = solve1();
ll ans1 = solve2();
cout << ans << " " << ans1 << "\n";
return 0;
}